Fast Perfect Hashing Of Integral Types

A perfect hash function is one that is collision-free. By implication, the hash must be at least as many bytes as the key and the function is theoretically reversible, though not always tractably so. In other words, perfect hashing is a special case of encryption. Because the hash is no smaller than the key, the primary use case is randomizing small values like integral types.

Below I describe an algorithm that takes 8-, 16-, 32-, or 64-bit keys and computes a high-quality key-sized hash in single-digit clock cycles that is collision-free. Other key sizes, such as 24-bits, are a trivial extension. The algorithm exploits the internal structure of the AES encryption algorithm to compute collision-free hashes that are smaller than the 128-bit AES block size using the AES instructions available on most modern CPUs.

On paper, the collision-free property of perfect hash functions can materially improve the design of some hash-based algorithms and data structures. In practice, these benefits have been offset by the large differences in computational cost between ordinary and perfect hash functions of similar quality. The algorithms presented below are much faster than most non-perfect hash functions on recent CPUs.

Encrypting a padded 32-bit value with AES will not produce a perfect 32-bit hash. AES is only guaranteed to be perfect if the key is 128-bits. Making the AES algorithm produce a perfect hash of, for example, a 32-bit key in its lowest 32 bits requires understanding the internals of the AES algorithm.

The 16 bytes of an AES block are logically organized as a 4x4 grid. A single round of AES, among other steps, logically rotates each 4-byte row…

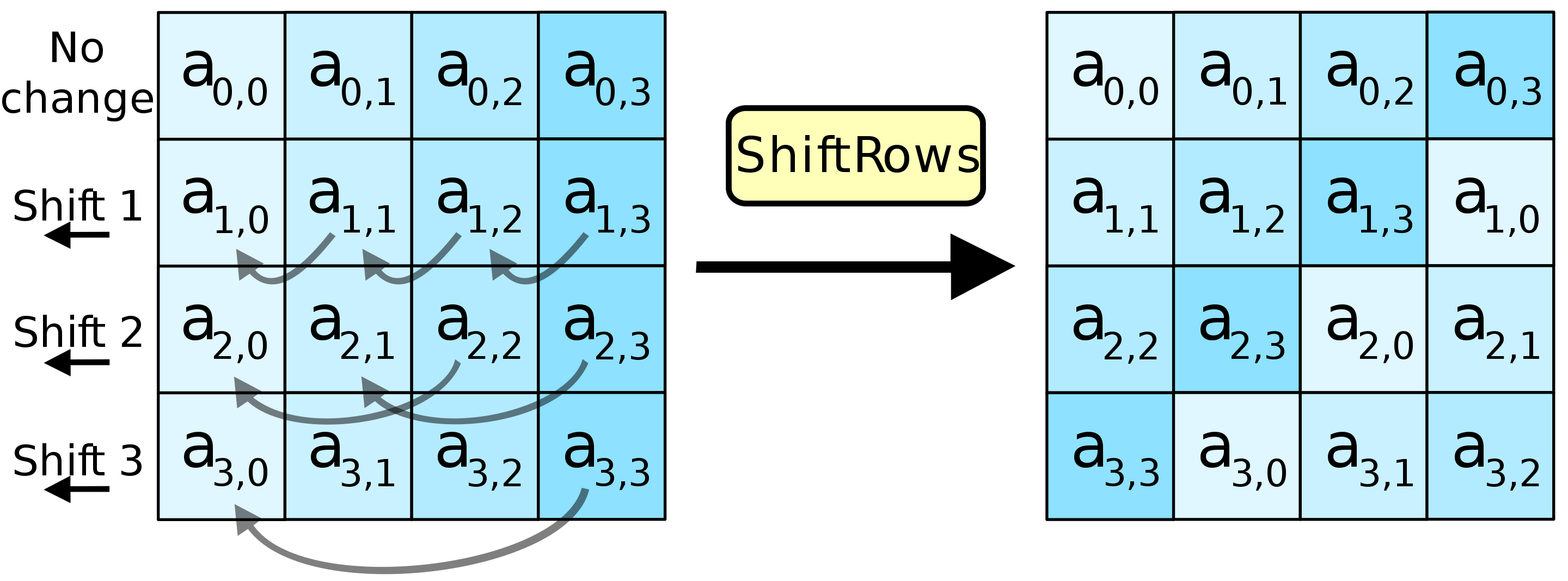
…and then mixes each 4-byte column.

In a sense, the algorithm works by doing four 32-bit encryptions in each round and mixing the results in subsequent rounds. If you represent a 32-bit key as a padded 128-bit AES block, it is straightforward to determine if a given byte in the key is mixed with a given byte in the 4x4 grid. For the purposes of perfect hashing, the objective is to mix every byte in the key with every byte in the part of the AES block that holds the hash. In the 32-bit case, it is apparent upon inspection that this objective cannot be met after a single round of AES by simply padding the key.

However, if you know which bytes from the 4x4 grid are mixed with each of the first four bytes of the AES block then you can distribute the key bytes across the 4x4 grid such that every hash byte is fully mixed with every key byte. While the details can vary with key size, the simplest solution is to use 128-bit broadcast instructions, which is what are used below.

All of the following algorithms put a perfect key-sized hash in the first bytes of a 128-bit AES block. Keys that are less than or equal to the size of a 4 byte AES column can be perfectly hashed in a single round of AES with an appropriate distribution of key bytes.

// 32-bit perfect hash
uint32_t hash32(uint32_t key) {
    __m128i hash_32 = _mm_set1_epi32(key);
    hash_32 = _mm_aesenc_si128(hash_32, _mm_set1_epi32(0xDEADBEEF));
    return *reinterpret_cast<uint32_t*>(&hash_32);
}

// 16-bit perfect hash
uint16_t hash16(uint16_t key) {
    __m128i hash_16 = _mm_set1_epi16(key);
    hash_16 = _mm_aesenc_si128(hash_16, _mm_set1_epi32(0xDEADBEEF));
    return *reinterpret_cast<uint16_t*>(&hash_16);
}

// 8-bit perfect hash
uint8_t hash8(uint8_t key) {
    __m128i hash_8 = _mm_set1_epi8(key);
    hash_8 = _mm_aesenc_si128(hash_8, _mm_set1_epi32(0xDEADBEEF));
    return *reinterpret_cast<uint8_t*>(&hash_8);
}

A 64-bit equivalent is slightly more complicated. We need to mix 8 key bytes but the 4x4 byte grid construction of the AES algorithm allows us to mix a maximum of four bytes in a single round. Adding a second AES round mixes each of the hash bytes, containing 4 of 8 key bytes, with hash bytes containing the complement key bytes, at the cost of a few more clock cycles.

// 64-bit perfect hash
uint64_t hash64(uint64_t key) {
    __m128i hash_64 = _mm_set1_epi64x(key);
    hash_64 = _mm_aesenc_si128(hash_64, _mm_set1_epi32(0xDEADBEEF));
    hash_64 = _mm_aesenc_si128(hash_64, _mm_set1_epi32(0xDEADBEEF));
    return *reinterpret_cast<uint64_t*>(&hash_64);
}

The 128-bit constant supplied as a second argument to the AES intrinsic is arbitrary. This value is XOR-ed with the hash as the final step of an AES round and therefore has no impact on quality.

The quality of these hashes is relatively high, as one might expect when using an AES round for hashing. It is also valid to apply more than one round of perfect hashing to strengthen the hash, though this has limited value in practice.

The underlying AES mechanics used to effect perfect hashing can also be used to construct an extremely high-performance ordinary hash function, which will be shown in a follow-on post.